Geometry is the branch of mathematics that explores the properties and relationships of shapes, sizes, and spaces. It's a discipline that has fascinated mathematicians, scientists, and thinkers for millennia. At its core, geometry helps us make sense of the world around us by studying the fundamental building blocks of our universe: points, lines, angles, and shapes. Let's delve into the major branches of geometry to gain a better understanding of this captivating field.

Major Branches of Geometry

Geometry isn't a one-size-fits-all concept; it encompasses various specialized branches, each focusing on distinct aspects of space and shape.

Here, we'll introduce you to some of the most prominent branches of geometry:

Euclidean Geometry

Euclidean geometry, named after the ancient Greek mathematician Euclid, is perhaps the most well-known branch of geometry. It deals with the properties of flat, two-dimensional shapes and the relationships between points, lines, and angles in a plane. Euclidean geometry forms the foundation of our understanding of geometry and serves as a basis for many practical applications in architecture, engineering, and art.

Analytic Geometry

Analytic geometry brings the power of algebra into the world of geometry. It combines algebraic equations with geometric shapes, allowing us to represent complex curves, lines, and figures using mathematical equations. This branch of geometry was developed by René Descartes and Pierre de Fermat in the 17th century and has since become an essential tool in fields like physics and engineering.

Projective Geometry

Projective geometry explores the properties of geometric objects that remain unchanged under projection or transformation. It has applications in computer graphics, computer vision, and art, often dealing with perspectives and vanishing points. Projective geometry challenges our intuition by considering parallel lines as intersecting at a point at infinity, leading to intriguing results.

Differential Geometry

Differential geometry delves into the study of curved surfaces and spaces. It's a branch of geometry with profound implications in physics, particularly in understanding the geometry of spacetime in Einstein's theory of relativity. Differential geometry plays a crucial role in fields like astronomy, cosmology, and general relativity, where it helps us grasp the curvature of the universe itself.

Non-Euclidean Geometries

Non-Euclidean geometries, including hyperbolic and elliptic geometries, challenge the assumptions of Euclidean geometry. In these geometries, the familiar Euclidean postulates don't hold, leading to fascinating results and paradoxes. These non-Euclidean systems have found applications in fields like art, architecture, and the theory of relativity.

Topology

Topology is the study of the properties of space that are preserved under continuous deformations, such as stretching or bending, but not tearing or gluing. It focuses on concepts like continuity, compactness, and connectedness. Topology plays a significant role in understanding the shape of objects without concerning themselves with distances and angles, making it an essential field in modern mathematics and physics.

Plane Geometry (Two-dimensional Geometry)

Now that we've explored the major branches of geometry let's zoom in on two fundamental dimensions - plane geometry. In this branch, we work with flat, two-dimensional shapes and examine the key terminologies that help us describe and analyze them:

📐
Points: Points are the most fundamental objects in geometry. They are represented as single dots and have no size or dimension. Think of them as the building blocks from which all geometric figures are constructed.
📐
Lines: Lines are straight paths that extend infinitely in both directions. They are composed of an infinite number of points and have no thickness. In geometry, lines are typically denoted by lowercase letters or symbols.
📐
Angles: Angles are formed when two lines or line segments intersect at a common point. They measure the amount of rotation required to align one line segment with another. Angles are essential for understanding the relationships between lines and shapes in geometry. Let's take a closer look at the significance of angles in geometry.

Angles in Geometry

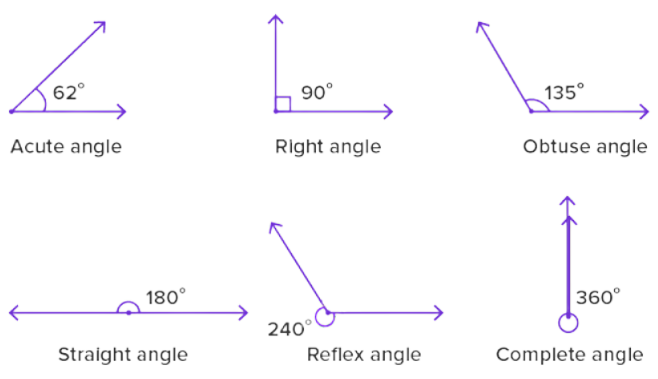
Angles are not just abstract concepts; they play a fundamental role in understanding the relationships between various geometric elements.

Here are some essential aspects of angles in geometry:

Angles are measured in degrees (°). A full rotation around a point corresponds to 360°. Angles can also be measured in radians in more advanced mathematical contexts.

Types of Angles: Angles come in various types, depending on their size and relationships. Some common types include:

  • Acute Angle: An angle smaller than 90°.
  • Right Angle: An angle equal to 90°, forming a perfect "L" shape.
  • Obtuse Angle: An angle greater than 90° but less than 180°.
  • Straight Angle: An angle equal to 180°, forming a straight line.
  • Reflex Angle: An angle greater than 180° but less than 360°.
  • Full Angle: An angle equal to 360°, representing a full rotation.
  1. Complementary and Supplementary Angles: Complementary angles add up to 90°, while supplementary angles add up to 180°. These relationships are essential in solving geometric problems involving angles.
  2. Angle Bisector: An angle bisector is a line or ray that divides an angle into two congruent (equal) angles. It's a valuable tool for constructing angles of specific measurements.
  3. Vertical Angles: Vertical angles are opposite angles formed by the intersection of two lines. They are always congruent, meaning they have the same measurement.
  4. Adjacent Angles: Adjacent angles share a common vertex and a common side but do not overlap. They can be supplementary or complementary, depending on their measurements.
  5. Interior and Exterior Angles: In polygons, interior angles are the angles formed inside the shape, while exterior angles are the angles formed outside the shape. Understanding these angles is crucial in polygon geometry.

Now that we've explored the significance of angles in plane geometry, let's transition to the world of solid geometry, where we venture into three dimensions.

Solid Geometry (Three-dimensional Geometry)

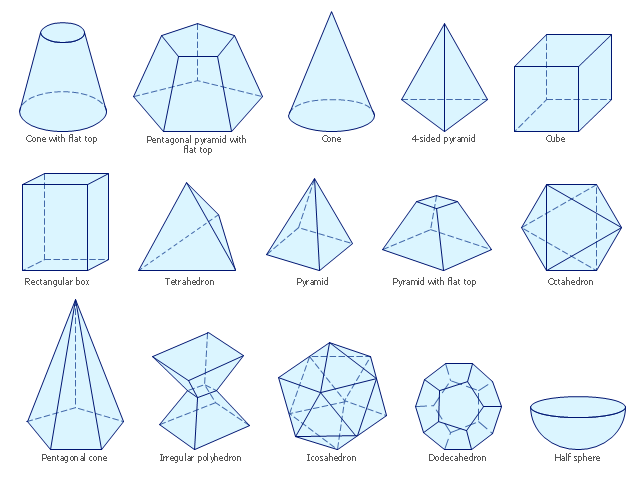
Solid geometry takes the principles of geometry into the third dimension, allowing us to study and analyze three-dimensional shapes and objects. While plane geometry deals with flat figures, solid geometry introduces us to the world of volume, depth, and three-dimensional forms. Here are some key aspects of solid geometry:

Three-Dimensional Shapes: Solid geometry explores a wide range of three-dimensional shapes, including:

  • Prisms: Polyhedra with two parallel and congruent polygonal bases connected by rectangular faces.
  • Pyramids: Polyhedra with a polygonal base and triangular faces converging at a common vertex.
  • Cylinders: Three-dimensional shapes with two circular bases and a curved surface connecting them.
  • Cones: Similar to cylinders but with a single circular base and a curved surface that narrows to a point.
  1. Volume and Surface Area: In solid geometry, we calculate the volume (space enclosed) and surface area (outer covering) of three-dimensional objects. Formulas for calculating these properties are crucial in various real-world applications, such as engineering and architecture.
  2. Euler's Formula: Euler's formula, also known as the Euler characteristic, relates the number of vertices, edges, and faces of a polyhedron. It plays a significant role in classifying and understanding three-dimensional shapes.
  3. Symmetry in 3D Shapes: Solid geometry often deals with symmetry and its impact on three-dimensional objects. Recognizing symmetrical properties is vital in design, art, and engineering.
  4. Solid Transformations: Transformations like translation, rotation, and reflection are key concepts in solid geometry. These transformations help us understand how three-dimensional shapes can be manipulated and changed.

In conclusion, geometry is a multifaceted field that spans numerous branches, each with its unique focus and applications. Whether you're exploring the elegance of Euclidean geometry, the complexities of non-Euclidean geometries, or the three-dimensional world of solid geometry, this mathematical discipline offers a rich tapestry of concepts and tools for understanding the shapes and spaces that surround us. Whether you're a mathematician, scientist, artist, or simply someone with a curiosity about the world, geometry invites you to explore the beauty of shapes and space from various angles and dimensions.

GET $15 OF FREE TUTORING WHEN YOU SIGN UP USING THIS LINK

Here are some frequently asked questions (FAQs) about geometry:

What is geometry, and why is it important?

Geometry is the branch of mathematics that studies shapes, sizes, and spaces. It's crucial because it helps us understand and describe the physical world, from designing buildings to exploring the cosmos.

What are the major branches of geometry, and how do they differ?

Geometry branches into Euclidean, Analytic, Projective, Differential, Non-Euclidean, and Topology, each focusing on different aspects of space and shape, from traditional plane geometry to the geometry of curved spaces.

How does Euclidean geometry differ from other types of geometry?

Euclidean geometry is the study of flat, two-dimensional shapes and the relationships between points, lines, and angles. Unlike non-Euclidean geometries, it adheres to Euclid's postulates, forming the basis of traditional geometric understanding.

Can you provide examples of real-world applications of geometry?

Geometry is applied in various fields, such as architecture, engineering, art, and physics. For instance, architects use geometric principles to design structures, and physicists apply geometry to understand the fabric of the universe.

What are the essential concepts in plane geometry?

Plane geometry focuses on two-dimensional shapes and introduces fundamental concepts like points, lines, and angles, which are the building blocks for describing and analyzing geometric figures.