Geometry, the study of shapes and their properties, is a fascinating branch of mathematics. Among its fundamental elements, rays play a crucial role. Rays are used to describe lines that originate from a specific point and extend infinitely in one direction. In this article, we will explore the meaning of rays in geometry, how to identify and name them, their properties, real-life examples, and their applications in various fields.
What Is A Ray?
In the realm of geometry, a ray holds a significant position as one of the fundamental elements used to describe lines and angles. It is a concept that allows us to extend the notion of a line segment infinitely in one direction. To grasp the essence of a ray, let's delve into its definition and key characteristics.
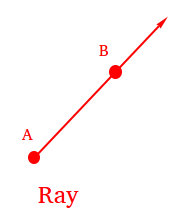
A ray can be defined as a part of a line that consists of a single endpoint, also known as the initial point, and extends infinitely in one direction. Imagine standing at a specific location and shooting an arrow in a straight line. The arrow represents a ray, with the starting point being the endpoint and the direction in which the arrow points symbolizing the extension of the ray. This visualization helps us understand that a ray has no end and continues indefinitely along a straight path.
The crucial elements in defining a ray are its endpoint and its direction of extension. The endpoint is the fixed location from which the ray originates. It acts as a starting point or anchor for the ray. The direction of extension is indicated by an arrowhead, emphasizing that the ray extends infinitely in a particular direction.
Rays can be observed in various geometric shapes and structures. For instance, consider a line segment AB. If we extend this line segment indefinitely in the direction away from point A, we obtain a ray. This ray is denoted as "Ray AB" or "Ray BA," signifying that it starts from point A and extends infinitely in the direction of point B. Similarly, we can identify and name other rays by specifying their endpoints and the direction in which they extend.
It is important to note that rays lack a measurable length because they continue infinitely. Unlike line segments, which have two distinct endpoints and a finite length, rays are unbounded. This unbounded nature is what sets rays apart and gives them their unique characteristics.
Real-Life Examples of Rays
Rays can be found in numerous real-life scenarios, often represented by objects or concepts that exhibit unidirectional movement or extension.
Here are some everyday examples of rays:
- Sunlight beaming through a window
- Laser beams projecting from a laser pointer
- Path of light reflecting off a mirror or a shiny surface
- Straight roadways stretching into the horizon
- Rays of light emanating from a distant star
What Is The Meaning of Ray in Geometry?
In the realm of geometry, rays are essential tools used to represent and analyze lines and angles. They provide a means to describe the direction and extent of a line segment, extending infinitely in one direction. Rays are considered one-dimensional and lack a measurable length since they continue indefinitely.
How Do You Identify a Ray in Geometry?
To identify a ray, there are two crucial elements to consider: the endpoint and the direction of extension. The endpoint is the fixed starting point from which the ray originates. The direction of extension is indicated by an arrowhead, illustrating the path in which the ray continues infinitely. By combining these elements, we can clearly identify and distinguish rays from other line segments.
Examples of Rays in Geometry
Rays can be observed in various geometric shapes and structures.
Here are a few examples:
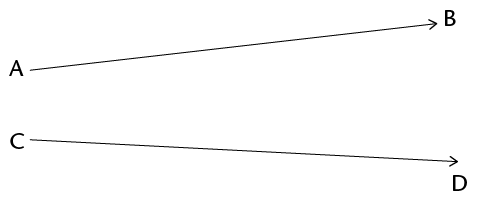
- Ray AB: Originating from point A and extending infinitely in the direction of point B.
- Ray CD: Extending infinitely in the direction from point C to point D.
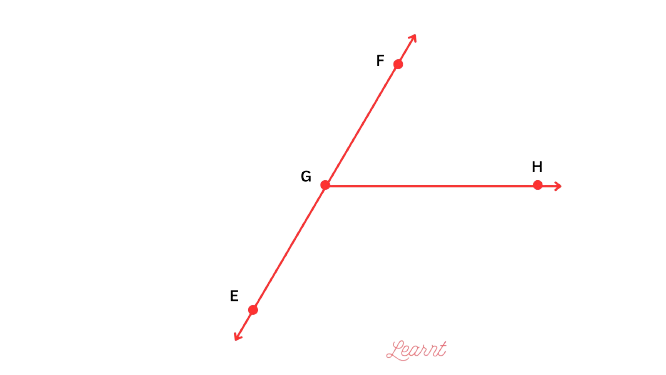
- Ray EF: Starting from point E and extending indefinitely in the direction of point F.
- Ray GH: Originating from point G and continuing infinitely towards point H.
Naming a Ray in Geometry
In geometry, rays are typically named using the endpoint and a random letter from another point on the ray. For instance, if a ray originates from point A and extends indefinitely towards point B, it can be named as "Ray AB" or "Ray BA." The choice of naming convention depends on the context and personal preference, as both representations indicate the same ray.
Properties of Rays
Rays possess several notable properties that are crucial to understanding their behavior within geometric systems:
Rays extend infinitely in one direction, without an endpoint on the other side.
Rays have a specific direction indicated by an arrowhead, signifying the path of extension.
Rays are considered one-dimensional, lacking measurable length.
Given an endpoint, there is only one ray extending infinitely in a particular direction.
Applications of Rays in Geometry
Rays find practical applications in various fields, including:
- Optics: Rays of light are used to study the behavior of light, including reflection, refraction, and dispersion.
- Architecture: The concept of rays assists architects in designing buildings and understanding the flow of natural light within a structure.
- Computer Graphics: Rays are employed in ray tracing algorithms to simulate the path of light and create realistic images in computer graphics.
Some Common Terms Related to Rays
In geometry, several terms are associated with rays, expanding our understanding of their characteristics and interactions with other geometric elements. These terms include:
- Collinear: Points lying on the same line or ray are said to be collinear.
- Intersection: The point where two rays or lines meet is known as their intersection.
- Angle: Rays are fundamental components in defining angles, which measure the amount of rotation between two rays with a common endpoint.
- Opposite Rays: Two rays with the same endpoint but extending in opposite directions are called opposite rays.
ConclusionRays play a significant role in geometry, providing a means to describe lines, angles, and their interactions. By understanding the properties and behavior of rays, we gain valuable insights into the foundations of geometric principles. From real-life examples to practical applications, rays find relevance in various fields, making them an essential concept in both theoretical and practical aspects of geometry. So next time you observe sunlight streaming through a window or gaze at the distant stars, remember that rays are the invisible threads connecting these phenomena to the world of geometry.

What is a ray in geometry?
In geometry, a ray is a part of a line that has a fixed starting point (endpoint) and extends infinitely in one direction. It can be visualized as an arrow that continues indefinitely along a straight path.
How do I identify a ray in geometry?
To identify a ray, you need to consider two important aspects: the endpoint (starting point) and the direction of extension. The endpoint is the fixed location where the ray originates, while the direction is indicated by an arrowhead, representing the infinite extension of the ray.
Can you provide some real-life examples of rays?
Certainly! Some everyday examples of rays include sunlight streaming through a window, laser beams projecting from a laser pointer, light reflecting off a mirror, straight roadways stretching into the horizon, and rays of light emanating from a distant star.
How are rays named in geometry?
In geometry, rays are typically named using the endpoint and a random letter from another point on the ray. For example, if a ray extends from point A towards point B, it can be named "Ray AB" or "Ray BA." The choice of naming convention depends on the context and personal preference.
How are rays used in geometry applications?
Rays have practical applications in various fields, including optics, architecture, and computer graphics. In optics, rays of light are studied to understand reflection, refraction, and dispersion. Architects use the concept of rays to design buildings and consider natural light flow. Computer graphics employ rays in ray tracing algorithms to create realistic images by simulating the path of light.





