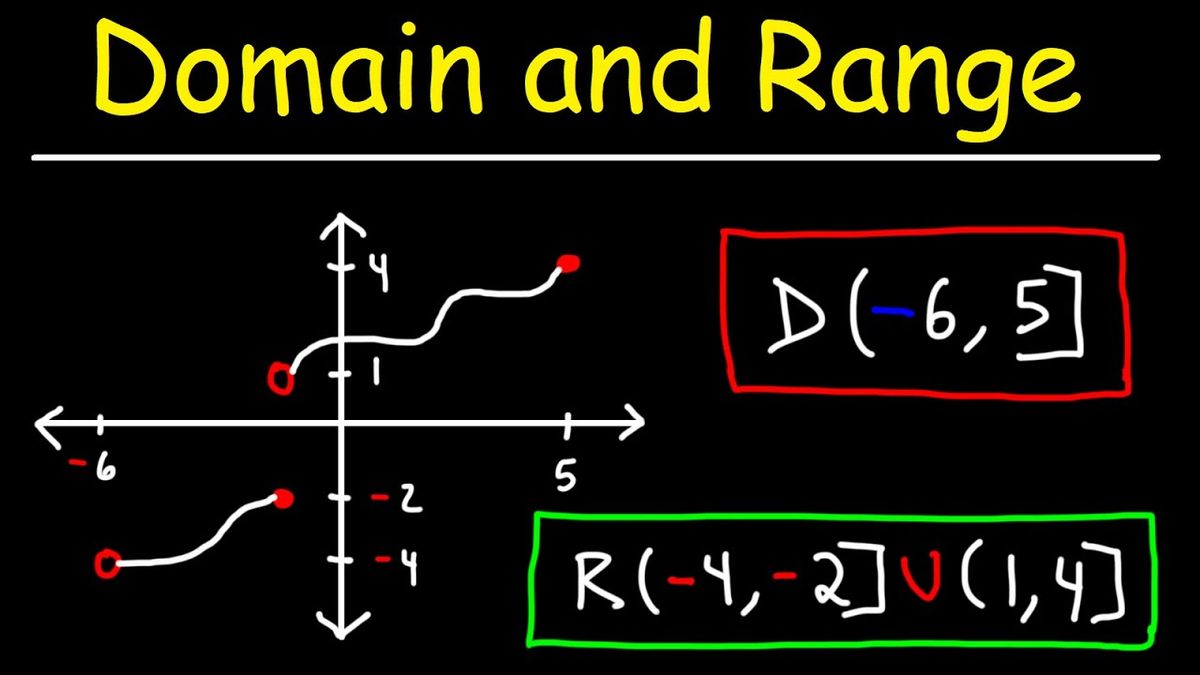
Domain and range are fundamental concepts in mathematics, particularly in studying functions. Understanding the domain and range of a function is crucial for solving problems in calculus, algebra, and other branches of mathematics.
In this article, we will explore what the functions of domain and range, how to find them, and their importance in mathematics.
What is the Domain of a Function?
The domain of a function is the set of all possible values of the independent variable for which the function is defined. In other words, it is the set of input values for which the function produces meaningful output. For example, consider the function f(x) = 1/x. The domain of this function is all real numbers except for x = 0, because the function is undefined at x = 0 due to division by zero.
The domain of a function can be expressed using interval notation. For example, if the domain of a function is all real numbers between -1 and 1, including -1 and 1, we can write the domain as [-1, 1].
It is important to note that not all functions have a domain that consists of all real numbers. For example, the square root function has a domain that consists of non-negative real numbers, because the square root of a negative number is not a real number.
How to Find the Domain of a Function?
To find the domain of a function, we need to consider the restrictions on the input variable that make the function undefined. Some common restrictions include:
• Division by zero: If a function contains a fraction in which the denominator equals zero, then the function is undefined for that value of the independent variable.
• Square roots: If a function contains a square root, then the radicand (the number inside the square root symbol) must be non-negative, otherwise the function is undefined.
• Logarithmic functions: If a function contains a logarithm, then the argument (the number inside the logarithm) must be positive, otherwise the function is undefined.
Once we have identified the restrictions on the input variable, we can express the domain of the function in interval notation. For example, if a function is undefined for x < 0, we can write the domain as [0, ∞).
What is the Range of a Function?
The range of a function is the set of all possible output values of the function. In other words, it is the set of values that the dependent variable can take on for different values of the independent variable. For example, consider the function f(x) = x^2. The range of this function is all non-negative real numbers because x^2 is always non-negative.
The range of a function can also be expressed using interval notation. For example, if the range of a function is all real numbers between -1 and 1, including -1 and 1, we can write the range as [-1, 1].
How to Find the Range of a Function?
To find the range of a function, we need to determine the set of all possible output values. One way to do this is to analyze the behavior of the function as the input variable varies. For example, if the function is a quadratic function, we can use the vertex form of the quadratic equation to determine the vertex and the axis of symmetry. The vertex gives us the minimum or maximum value of the function, and the axis of symmetry tells us where the function is symmetric.
Another way to find the range of a function is to use calculus. If the function is differentiable, we can find the critical points (where the derivative is equal to zero or undefined) and the endpoints of the domain. We can then evaluate the function at these points to determine the maximum and minimum values and thus the range of the function.
It is important to note that not all functions have a range that consists of all real numbers. For example, the function f(x) = sin(x) has a range that is bounded between -1 and 1, because the sine function oscillates between these values.
Why is the Domain and Range Important?
The domain and range of a function are important because they help us understand the behavior of the function and its limitations. For example, the domain of a function tells us which values of the independent variable we can plug into the function to get a meaningful output. If we try to evaluate the function outside its domain, we may get an error or an undefined value.
Similarly, the range of a function tells us which values of the dependent variable we can obtain from the function. If the range is bounded, it tells us that the function can never take on certain values, which may be important for interpreting the results of a problem.
In addition, the domain and range of a function are important for graphing the function. By knowing the domain and range, we can determine the maximum and minimum values of the function, which can help us plot the graph accurately. Furthermore, by analyzing the domain and range, we can identify any discontinuities, holes, or asymptotes in the graph of the function.
Examples of Domain and Range
Let's look at some examples of functions and their domains and ranges.
f(x) = 1/x
The domain of this function is all real numbers except for x = 0, because the function is undefined at x = 0 due to division by zero. The range of this function is all real numbers except for 0, because as x approaches 0, 1/x approaches infinity or negative infinity.
f(x) = x^2.
The domain of this function is all real numbers, because x^2 is defined for all real numbers. The range of this function is all non-negative real numbers, because x^2 is always non-negative.
f(x) = sqrt(x)
The domain of this function is all non-negative real numbers, because the square root of a negative number is not a real number. The range of this function is all non-negative real numbers, because the square root of a non-negative number is always non-negative.
f(x) = sin(x)
The domain of this function is all real numbers, because the sine function is defined for all real numbers. The range of this function is bounded between -1 and 1, because the sine function oscillates between these values.
Conclusion
In conclusion, the domain and range of a function are important concepts in mathematics that help us understand the behavior and limitations of a function.
The domain is the set of all possible values of the independent variable for which the function is defined, while the range is the set of all possible output values of the function. By analyzing the domain and range of a function, we can graph the function accurately, identify any discontinuities or asymptotes, and interpret the results of a problem.

Frequently Asked Questions (FAQs) About Domain and Range
What is the domain of a function?
The domain of a function is the set of all possible values of the independent variable for which the function is defined.
What is the range of a function?
The range of a function is the set of all possible output values of the function.
Why is domain and range important?
Domain and range are important because they help us understand the behavior of the function and its limitations. They also help us graph the function accurately and interpret the results of a problem.
How do you find the domain of a function?
To find the domain of a function, we need to look for any values of the independent variable that would make the function undefined. Common examples include division by zero and taking the square root of a negative number.
How do you find the range of a function?
To find the range of a function, we need to look for all possible output values of the function. This can sometimes be determined by analyzing the behavior of the function, such as whether it is increasing or decreasing.
Can a function have an infinite domain or range?
Yes, a function can have an infinite domain or range. For example, the function f(x) = 1/x has an infinite domain and range.