The Power of Supplementary Angles: Applications in Math and Science

In geometry, angles are one of the essential concepts that form the basis of many mathematical problems and constructions. An angle is formed by two rays that share a common endpoint, known as the vertex. The measure of an angle is typically expressed in degrees, with a full circle consisting of 360 degrees.

In this article, we will explore the concept of supplementary angles, including their properties, characteristics, and applications.

Properties of Supplementary Angles

1. Sum of Measures
   The sum of the measures of two supplementary angles is always 180 degrees. This property is fundamental to the definition of supplementary angles and is used in many mathematical proofs and constructions.
   
2. Complementary Angles
   Supplementary angles can be contrasted with complementary angles, which are two angles whose sum is 90 degrees. Complementary angles are commonly found in right triangles, where one of the angles is a right angle.
   
3. Angle Bisectors
   Supplementary angles are often used in constructing angle bisectors. An angle bisector is a line or ray that divides an angle into two equal parts. To construct an angle bisector, we need to draw a line or ray that splits the angle into two supplementary angles.
   
4. Parallel Lines
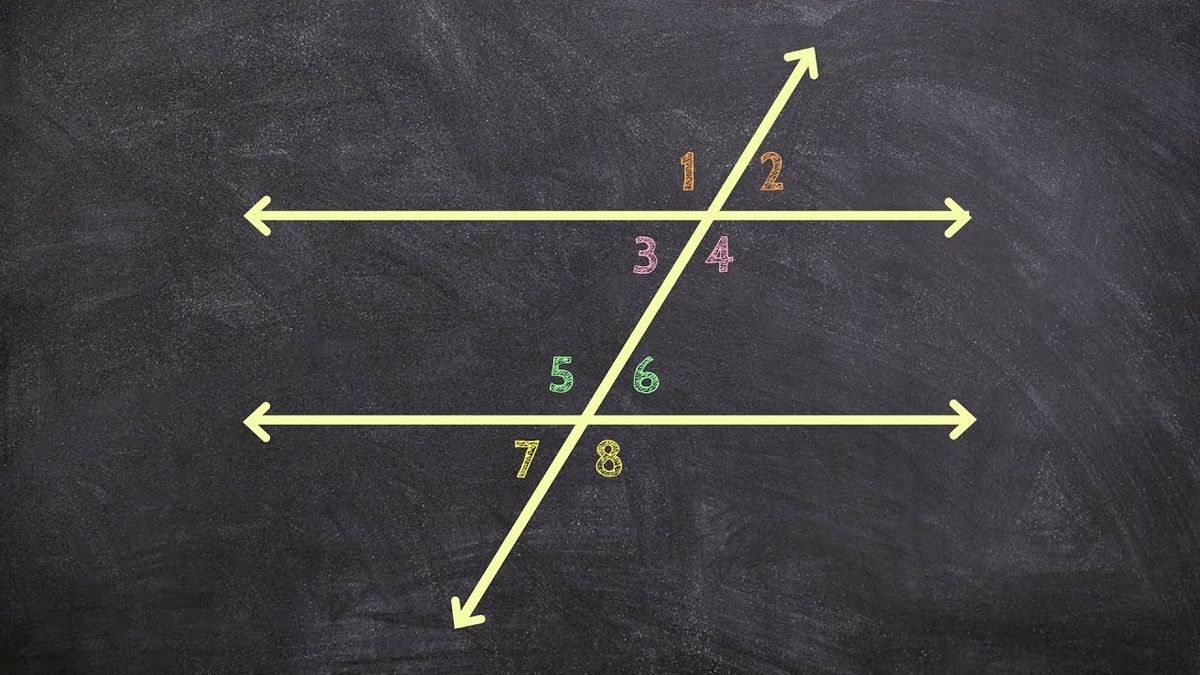
   Supplementary angles can also be used to prove that two lines are parallel. If two lines are intersected by a transversal, and the alternate interior angles are congruent, then the lines are parallel. The alternate interior angles are supplementary, so if they add up to 180 degrees, then the lines are parallel.

Applications of Supplementary Angles

1. Trigonometry
   Supplementary angles are commonly used in trigonometry to find the values of trigonometric functions such as sine, cosine, and tangent. The relationships between the angles and sides of a right triangle are based on the properties of supplementary angles.
   
2. Physics
   In physics, supplementary angles are used to describe the orientation of objects in space. For example, the pitch and roll angles of an airplane are two supplementary angles that describe the orientation of the aircraft in three-dimensional space.
   
3. Architecture
   Supplementary angles are used in architecture to design structures that are aesthetically pleasing and functional. In designing buildings, architects use the principles of supplementary angles to create angles that are visually appealing and structurally sound.
   
4. Engineering
   Supplementary angles are also used in engineering, particularly in the design of mechanical systems. Engineers use the principles of supplementary angles to design machines that operate smoothly and efficiently.

Real-World Examples of Supplementary Angles

Supplementary angles are not just an abstract concept used in geometry and trigonometry – they also have real-world applications. For example, in construction and engineering, supplementary angles are used to determine the angles of walls, roofs, and other structures. By knowing the angle of one surface, you can use supplementary angles to determine the angle of the adjacent surface.

Supplementary angles are also used in navigation and surveying. For example, if you know the angle between two landmarks and the angle between one of the landmarks and a third point, you can use supplementary angles to determine the angle between the third point and the second landmark.

Supplementary angles are also used in art and design. Artists and designers use supplementary angles to create compositions that are visually appealing and balanced. By using angles that add up to 180 degrees, they can create a sense of harmony and balance in their work.

Conclusion

Supplementary angles are an important concept in geometry and trigonometry. They are two angles whose sum equals 180 degrees, and they have several important properties and applications. By understanding the properties and applications of supplementary angles, you can solve problems involving angles, polygons, and trigonometric functions, as well as apply them to real-world situations in construction, navigation, surveying, and art and design.

Frequently Asked Questions (FAQs) About Supplementary Angles