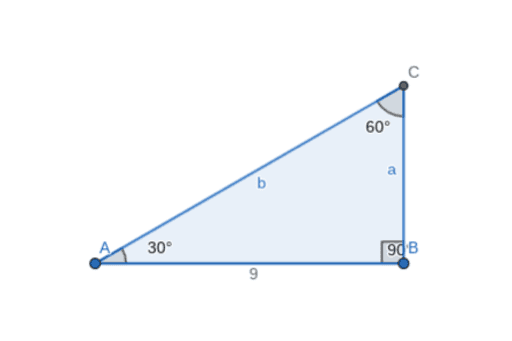
The 30-60-90 triangle is a special right triangle with angles of 30 degrees, 60 degrees, and 90 degrees. This triangle has some unique properties that make it useful in geometry, trigonometry, and other branches of mathematics.
In this article, we will explore the 30-60-90 triangle in detail, including its properties, formulas, and applications. We will see how it can be used to solve problems in geometry, trigonometry, and other fields, and how it fits into the broader context of mathematics.
Properties of the 30-60-90 Triangle
The 30-60-90 triangle is a right triangle with one angle measuring 90 degrees and the other two angles measuring 30 degrees and 60 degrees, respectively. The side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is √3/2 times the length of the hypotenuse.
One of the most useful properties of the 30-60-90 triangle is that it is always in a specific ratio. Specifically, the length of the hypotenuse is always twice the length of the shorter leg, and the length of the longer leg is always √3 times the length of the shorter leg. This means that if you know the length of one side of a 30-60-90 triangle, you can use these ratios to find the lengths of the other sides.
Formulas for the 30-60-90 Triangle
There are several formulas that can be used to calculate the lengths of the sides of a 30-60-90 triangle. One of the most basic is the Pythagorean theorem, which states that in any right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse.
Using the Pythagorean theorem, we can derive the following formulas for the 30-60-90 triangle:
• If the shorter leg of the triangle has length x, then the hypotenuse has length 2x, and the longer leg has length √3x.
• If the hypotenuse of the triangle has length h, then the shorter leg has length h/2, and the longer leg has length h√3/2.
The 30-60-90 triangle has numerous applications in mathematics and beyond. Here are just a few examples:
• Geometry: The 30-60-90 triangle can be used to solve problems involving similar triangles, parallel lines, and congruent angles.
• Trigonometry: The 30-60-90 triangle can be used to derive the values of sine, cosine, and tangent for angles of 30 degrees and 60 degrees. For example, the sine of 30 degrees is 1/2, and the cosine of 60 degrees is 1/2.
• Engineering: The 30-60-90 triangle is used in engineering and architecture to create structures with specific angles and dimensions. For example, a 30-60-90 triangle can be used to create a roof with a 30-degree pitch.
• Physics: The 30-60-90 triangle can be used in physics to calculate the angles and forces involved in various types of motion, such as projectile motion or circular motion.

Conclusion
In conclusion, the 30-60-90 triangle is a special right triangle with unique properties that make it a useful tool in various fields of mathematics and science. Its ratios and formulas can be applied in geometry, trigonometry, and physics to solve a range of problems involving measurements of angles, sides, and areas. Understanding the properties of this triangle is essential for students of mathematics and science, as it provides a strong foundation for more complex topics in these fields.
By mastering the concepts of the 30-60-90 triangle, students can develop their problem-solving skills and gain a deeper understanding of the relationships between angles and sides in different geometric shapes. Moreover, the triangle's properties and formulas can be applied in real-world situations, such as architecture, engineering, and navigation, where accurate measurements and calculations are critical.
Overall, the 30-60-90 triangle is a fascinating topic to explore and is an essential component of any math or science curriculum. With its unique properties and practical applications, it is sure to continue to intrigue and challenge students and professionals alike for years to come.
Frequently Asked Questions (FAQs) About 30-60-90 Triangle:
What is a 30-60-90 triangle?
A 30-60-90 triangle is a special right triangle where one angle measures 30 degrees, one angle measures 60 degrees, and the right angle measures 90 degrees. The sides of the triangle are in a fixed ratio of 1:√3:2, with the hypotenuse being twice as long as the shortest side.
How do you find the length of the sides in a 30-60-90 triangle?
To find the length of the sides in a 30-60-90 triangle, you can use the ratios of 1:√3:2. If you know the length of one side, you can find the lengths of the other two sides by multiplying or dividing by the appropriate ratio. For example, if the shortest side is 5 units long, the longer leg is 5√3 units long, and the hypotenuse is 10 units long.
How do you solve problems involving the 30-60-90 triangle?
To solve problems involving the 30-60-90 triangle, you can use the ratios and formulas that are specific to this triangle. You can also use trigonometric functions, such as sine, cosine, and tangent, to find the lengths of the sides and angles. It is important to understand the properties of the triangle and how they relate to each other in order to solve problems effectively.