Angles are fundamental geometric elements that play a crucial role in various mathematical concepts and real-world applications. Among the different types of angles, supplementary angles hold a special significance. In this article, we will delve into the world of supplementary angles, exploring their definition, types, properties, and how they can be utilized in problem-solving. Whether you're a student, educator, or simply curious about mathematics, this article will provide you with a comprehensive understanding of supplementary angles.
What are Supplementary Angles?
Supplementary angles are a pair of angles that, when combined, sum up to 180 degrees. In other words, they form a straight line when placed adjacent to each other. When two angles are supplementary, they complement each other perfectly, creating a linear relationship. This property makes supplementary angles a vital concept in geometry and trigonometry.
Four Angle Types
Supplementary angles can be classified into four different types based on their relative positions and measurements:
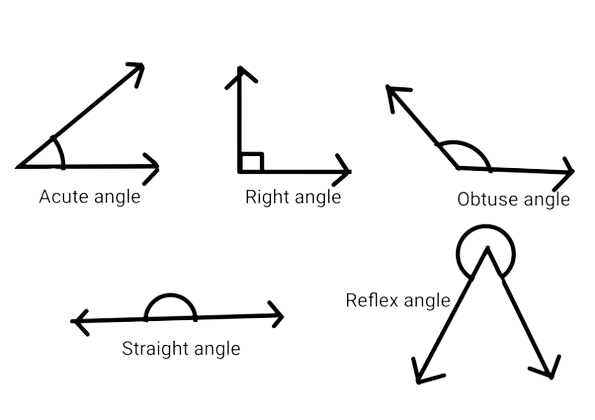
- Acute Angles: Acute supplementary angles are two angles that individually measure less than 90 degrees, but their sum equals 180 degrees. For example, if angle A measures 40 degrees, angle B would measure 140 degrees to form a pair of acute supplementary angles.
- Obtuse Angles: Obtuse supplementary angles consist of two angles, each measuring more than 90 degrees, yet their sum equals 180 degrees. For instance, if angle C measures 120 degrees, angle D would measure 60 degrees, resulting in a pair of obtuse supplementary angles.
- Right Angles: Right angles can also be supplementary to one another. When two right angles, each measuring 90 degrees, are combined, they form a pair of supplementary angles. This characteristic makes right angles a special case within the supplementary angle category.
- Straight Angles: Straight angles are the most prominent example of supplementary angles. A straight angle is formed when two opposite rays align perfectly, creating a line. It measures 180 degrees, signifying a complete rotation. As a result, a straight angle can be seen as a pair of supplementary angles with each angle measuring 180 degrees.
Examples of Supplementary Angles
To further solidify our understanding, let's explore a few examples of supplementary angles:
Consider two angles, one measuring 80 degrees and the other measuring 100 degrees. Although they differ in magnitude, their sum equals 180 degrees, making them a pair of supplementary angles.
Imagine we have two angles, one measuring 120 degrees and the other measuring 60 degrees. Despite being unequal, their sum again reaches 180 degrees, indicating that they form a pair of supplementary angles.
Now let's examine two right angles, each measuring 90 degrees. Combining these angles will always result in a sum of 180 degrees, illustrating their supplementary nature.
By studying these examples, we can observe how different types of angles can combine to form supplementary angles, regardless of their individual measurements.
Properties of Supplementary Angles
Supplementary angles possess several interesting properties that make them valuable tools in mathematical calculations. Some of these properties include:
- Angle Equality: The sum of the measures of two supplementary angles is always 180 degrees. This property remains constant regardless of the angle types or their individual measurements.
- Angle Complements: Each angle within a pair of supplementary angles acts as the complement of the other. In other words, if angle A is the complement of angle B, then angle B is the complement of angle A.
- Angle Addition: Supplementary angles can be combined or added together to form a straight angle, which measures 180 degrees. This property allows us to perform calculations and solve problems involving supplementary angles with ease.
- Unique Pairing: Given an angle, there exists only one other angle that can be paired with it to form a supplementary angle. This pairing ensures that the sum of the angles is always 180 degrees.
Understanding these properties will assist you in recognizing and utilizing supplementary angles effectively in various mathematical contexts.
Adjacent and Non-Adjacent Supplementary Angles
Supplementary angles can be further classified into two categories based on their spatial relationship: adjacent and non-adjacent supplementary angles.
Adjacent Supplementary Angles
Adjacent supplementary angles are two angles that share a common vertex and a common side, while their non-shared sides form a straight line. This means that the angles are adjacent to each other, with no space between them. The sum of adjacent supplementary angles always equals 180 degrees. Understanding adjacent supplementary angles is particularly useful when dealing with shapes and figures in geometry.
Non-adjacent Supplementary Angles
Non-adjacent supplementary angles, on the other hand, are two angles that do not share a common vertex or side. These angles are located at different points, with other elements lying between them. However, their sum remains constant at 180 degrees. Non-adjacent supplementary angles are often encountered when solving problems involving intersecting lines or angles within polygons.
How to Find Supplementary Angles?
Finding supplementary angles involves determining the measurement of one angle when the measurement of the other is known. The following steps outline the process:
- Identify the given angle: Begin by identifying the angle for which the measurement is known.
- Subtract the known angle from 180 degrees: Since the sum of supplementary angles is always 180 degrees, subtract the measurement of the known angle from 180 to find the measurement of the other angle.
- Verify the solution: Check if the sum of the two angles indeed equals 180 degrees to confirm the accuracy of your calculation.
By following these steps, you can find the measurement of supplementary angles and solve related problems efficiently.
Supplementary Angles Theorem
The Supplementary Angles Theorem is a fundamental theorem that states the following:
If two angles are supplementary to the same angle (or congruent angles), then they are congruent to each other.
This theorem provides an important relationship between congruent angles and supplementary angles. By utilizing this theorem, you can determine the congruence of angles based on their supplementary properties, simplifying geometric proofs and deductions.
Complementary vs. Supplementary
It is essential to distinguish between complementary angles and supplementary angles, as they serve distinct purposes in geometric calculations.
Complementary angles are a pair of angles that add up to 90 degrees. In contrast, supplementary angles sum up to 180 degrees. While complementary angles form a right angle when combined, supplementary angles form a straight angle.
Understanding this difference is crucial when solving problems involving angles and their relationships, ensuring accurate calculations and interpretations.
Conclusion
Supplementary angles play a vital role in geometry, trigonometry, and various real-world applications. By grasping their definition, properties, and classifications, you can confidently navigate the realm of supplementary angles. Whether you are examining adjacent or non-adjacent supplementary angles, using the Supplementary Angles Theorem, or discerning between complementary and supplementary angles, the knowledge you have gained will empower you to solve problems and make connections within the vast field of mathematics. Remember to practice applying these concepts to solidify your understanding and unlock the potential of supplementary angles in your mathematical journey.

FAQs About Supplementary Angles
What are supplementary angles?
Supplementary angles are a pair of angles that, when combined, add up to 180 degrees. They form a straight line when placed adjacent to each other.
What are the different types of supplementary angles?
Supplementary angles can be classified into four types: acute supplementary angles, obtuse supplementary angles, right angles (which are always supplementary to each other), and straight angles (which are a pair of supplementary angles measuring 180 degrees).
How can I identify adjacent supplementary angles?
Adjacent supplementary angles share a common vertex and a common side, while their non-shared sides form a straight line. They are angles that are adjacent to each other, with no space between them.
How can I identify non-adjacent supplementary angles?
Non-adjacent supplementary angles are angles that do not share a common vertex or side. They are located at different points, with other elements lying between them.
How can I find the measurement of a supplementary angle?
To find the measurement of a supplementary angle, subtract the known angle's measurement from 180 degrees. The resulting value will be the measurement of the other angle in the pair.






