The slope formula is a fundamental concept in mathematics and science that helps to describe the rate of change of a line. It is an important tool for analyzing data and understanding the relationships between variables.
Understanding the Slope Formula
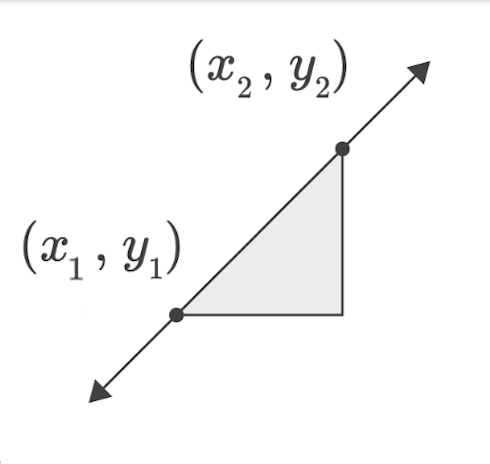
The slope formula is used to calculate the slope of a line, which is a measure of how steep or flat the line is. The formula is expressed as:
slope = (y2 - y1) / (x2 - x1)
where (x1, y1) and (x2, y2) are two points on the line. The slope formula can be applied to any two points on a line, and it is important to note that the order in which the points are selected does not affect the value of the slope.
The slope formula can also be written as:
slope = rise / run
where "rise" represents the change in the y-coordinate and "run" represents the change in the x-coordinate. This interpretation of the slope formula is useful for understanding the concept of slope as a rate of change.
Applications in Mathematics
The slope formula is an important tool in many areas of mathematics. Here are just a few examples:
Analyzing Graphs
The slope formula can help to identify patterns and relationships between variables, and it can be used to make predictions about future data points.
Calculus
The slope formula is used in calculus to calculate the derivative of a function. The derivative is a measure of how quickly a function is changing at a given point, and it is an important concept in calculus.
Geometry
The slope formula can be useful for determining the angles between lines and the lengths of line segments.
Using the Slope Formula Effectively
To use the slope formula effectively, it is important to be comfortable with basic algebraic operations such as subtraction, division, and multiplication. Here are some tips for using the slope formula effectively:
1. Choose Two Points
To use the slope formula, you need to choose two points on the line. It is important to choose points that are easy to work with, such as points with integer coordinates.
2. Label the Points
Once you have chosen your points, label them as (x1, y1) and (x2, y2). It is important to keep track of which point corresponds to which coordinate.
3. Plug in the Values
Once you have labeled your points, plug in the values into the slope formula. Make sure to subtract the y-coordinates and x-coordinates in the correct order.
4. Simplify the Expression
Once you have plugged in the values, simplify the expression by dividing the numerator and denominator by any common factors.
5. Interpret the Result
Finally, interpret the result. The slope represents the rate of change of the line, which can have different meanings depending on the context. For example, in a physics problem, the slope might represent the velocity of an object, while in a biology problem, it might represent the growth rate of a population.
In addition to using the slope formula to calculate the slope of a line, it is also important to understand the different types of slopes. A positive slope indicates that the line is increasing from left to right, while a negative slope indicates that the line is decreasing from left to right. A zero slope indicates that the line is horizontal, while an undefined slope indicates that the line is vertical.


Real-World Applications of the Slope Formula
The slope formula has many real-world applications that can be useful in everyday life. Here are a few examples:
Construction
The slope formula can be used to calculate the slope of a roof or a ramp. This can help to ensure that the roof or ramp is safe and functional.
Finance
The slope formula can be used to analyze financial data, such as the change in stock prices over time. This can help to make predictions about future trends and to make informed investment decisions.
Sports
The slope formula can be used to analyze sports data, such as the performance of athletes over time. This can help coaches and trainers to identify areas for improvement and to develop effective training plans.
Conclusion
The slope formula is a fundamental concept in mathematics and science that helps to describe the rate of change of a line. It has many applications in a variety of fields, including physics, chemistry, biology, finance, and sports.
By understanding the slope formula and its applications, we can analyze data, make predictions, and solve real-world problems.
Frequently Asked Questions about The Slope Formula:
What is the slope formula in math?
The slope formula in math is a way to calculate the steepness or inclination of a line. It is represented as (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
Why is the slope formula important in math?
The slope formula is important in math because it helps us understand the properties of lines, such as their direction and steepness. It is used in various fields, including physics, engineering, and economics, to analyze data and make predictions.
How do I find the slope of a line using the slope formula?
To find the slope of a line using the slope formula, you need to first identify two points on the line. Then, substitute the coordinates of these points into the formula and simplify the expression. The resulting value will be the slope of the line.
What does a positive slope mean in the slope formula?
A positive slope in the slope formula means that the line is sloping upwards from left to right. In other words, as the value of x increases, the value of y also increases. This indicates a positive correlation between the variables represented by x and y.
What does a negative slope mean in the slope formula?
A negative slope in the slope formula means that the line is sloping downwards from left to right. In other words, as the value of x increases, the value of y decreases. This indicates a negative correlation between the variables represented by x and y.