Ratios are the way to solve problems. When we have two things that are mathematically similar, most of us have seen ratios before. However, there's some tricks I'd like to show you that'll help you do them faster and more accurately.
We use ratios when we have two quantities, both of which are known for one case, one of which is known for the other. There's a number of ways to set things up. But I like to put one quantity on the top and the second quantity on the bottom, I put the known values on the left and the unknown value on the right standardizing, how you set up a ratio will make it less likely that you mess it up.
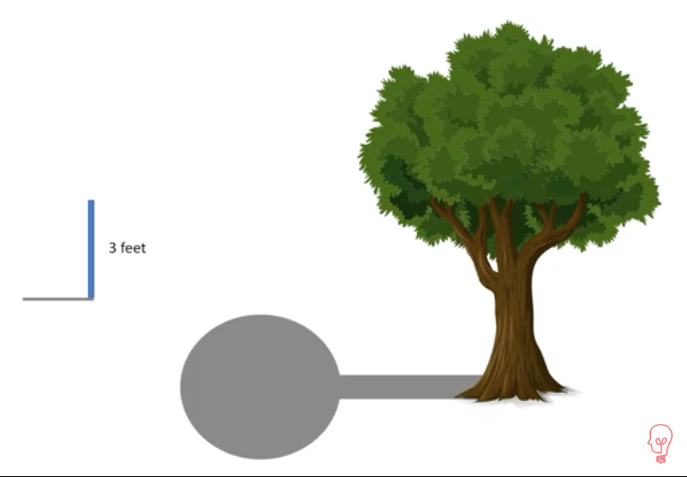
Now let's look at how to use them. Imagine that we wanna know the height of a tree, but all we have is a yard stick. Trying to measure the height of a tree with a yard stick is a non-trivial problem. We notice that both the yard stick and the tree cash shadows, which can easily be measured, that gives us enough information to use ratios. Let's see how to do it. Our two quantities are height and shadow length. It doesn't matter which we put on the top and which we put on the bottom. We just have to pick one and stick with it. Let's put the height on the top. Now we enter the values. We know both the height and the shadow length for the yard stick. So that goes on the left. We put the shadow length for the tree on the bottom of the right ratio. Let's see how to solve it.

When we first learned to do S in school, we learned to cross multiply and sell for X. While that always gives us a correct answer. It usually isn't the easiest way to do the problem. And it takes a lot more math than we really need to use. If we really look at this, what we're doing here is finding a fraction that has 16 on the bottom that has the same value as the one on the left. We can solve it by looking for patterns. In this case, we know that to get from two to 16, we need to multiply by eight. So we can sell for X by multiplying the three by eight, to get an answer of 24 feet. The tree is 24 feet tall.
Let's look at another example. I was shopping on the day after Valentine's day and found chocolates on sale. There are two boxes from the same company, one large, and one small. Now I can rationalize buying candy on sale, but since I'm overweight, I need to consider buying the small box. The number of pieces on the small box was covered up by the sale tag and only the weight was visible. However, we have both the number of pieces and the weight for the large box. How can I find out how many pieces are in the small box?
We set up our ratio with a number of pieces on the top and the weight on the bottom, the known values go on the left and the unknown on the right now let's solve it. Cross multiplying will give us the answer, but it requires us to multiply 32 by four and then divide by 16. That's more math than I wanna do. Looking for patterns. I can see that we can get from 16 to four by dividing by 4 30, 2 divided by four is eight. However, that's not the only way to make this one simple one rule of thumb I use is to take the numbers I work with and make them as small as possible because it's much easier to make mistakes with big numbers.
So let's simplify the 32 over 16 fraction to two over one. Then we can go from one to two by multiplying by two, we then use the same function on the right multiplying four times two to get eight. This method works both horizontally and vertically. As long as you do the same thing on both sides, all three methods work. It's just a matter of what patterns you recognize. The quickest maps are another place we use. Ratios maps have scales, which convert real distance to map distance. This provides us with the two known values. We can then measure the distance on the map. For example, Chicago, to Los Angeles and use ratios to convert that to real distance. We write the ratios and then look at them. We can cross-multiply simplify the left side. So we have the scale in whole inches, which gives us one inch equals 500 miles, then multiply by three and add two 50 for the half. We can notice that 0.5 times seven is 3.5 and multiply two 50 by seven. How we choose to do it depends on what patterns we see. And if we have a calculator handy or not, the purple way is faster. If you already have a calculator out or really good at multiplication, but the blue way is easier to do in your head.
Let's review the steps. First, we set up the ratio with the known quantities on one side and the unknown on the other. Then we look for patterns. If we find one, we can solve the problem right away. If not, we can simplify the ratio if possible, and look for patterns again. If we find one, we solve the problem. If we can't, we have to go back to the cross multiplying method. In the next video, I'll be giving you some problems, having you pause the video while you work on them and then restart the video to see the answers.