Connect with Brian
Welcome today. We are discussing the power rule of derivatives, which in order to basically understand the material in this lesson, it is advisable that you first be familiar with the limit rule of limit definition of derivatives, the constant multiple rule of derivatives and the sum rule of derivatives. So the lastly are quite easy.
So first the rule itself. So the power rule states that the would D with a over DX of X to the end equals N times X to the power of N minus one here N can actually be any number. But in practice, we are going to just be looking at the case today for when it isn't when, and is a whole number. So the proof is as follows. We first write out the limit definition of deriv of the derivative. Next we expand out the term X plus H all to the power of all to the power of N into a partially expanded sum of terms. Now, we do it as, as follows. We write X to the N plus H times, N times X to the N minus one. And now for the rest of the terms, we aren't really concerned about terms with X of lower degree. So we just write H to the second times a where a is a standard for the other terms, minus X to the N now, okay. Now X to the end, a negative X to the end cancel.

So this leaves us with now dividing out the common factor of H we get that this is equal to the limit of which is equal to N X and minus one, plus a zero or, and X and minus one. So that's the proof. It's very straightforward, nothing really much to it. So for some examples, we have D over DX X to the second equals two times X, the power of two minus one or two times X, D over D X, X to the third equals three X to the second to the third minus one, or three X to the second and D over D X, X to the 10th equals 10 times X to the power of 10 minus one or 10 times X to the ninth.
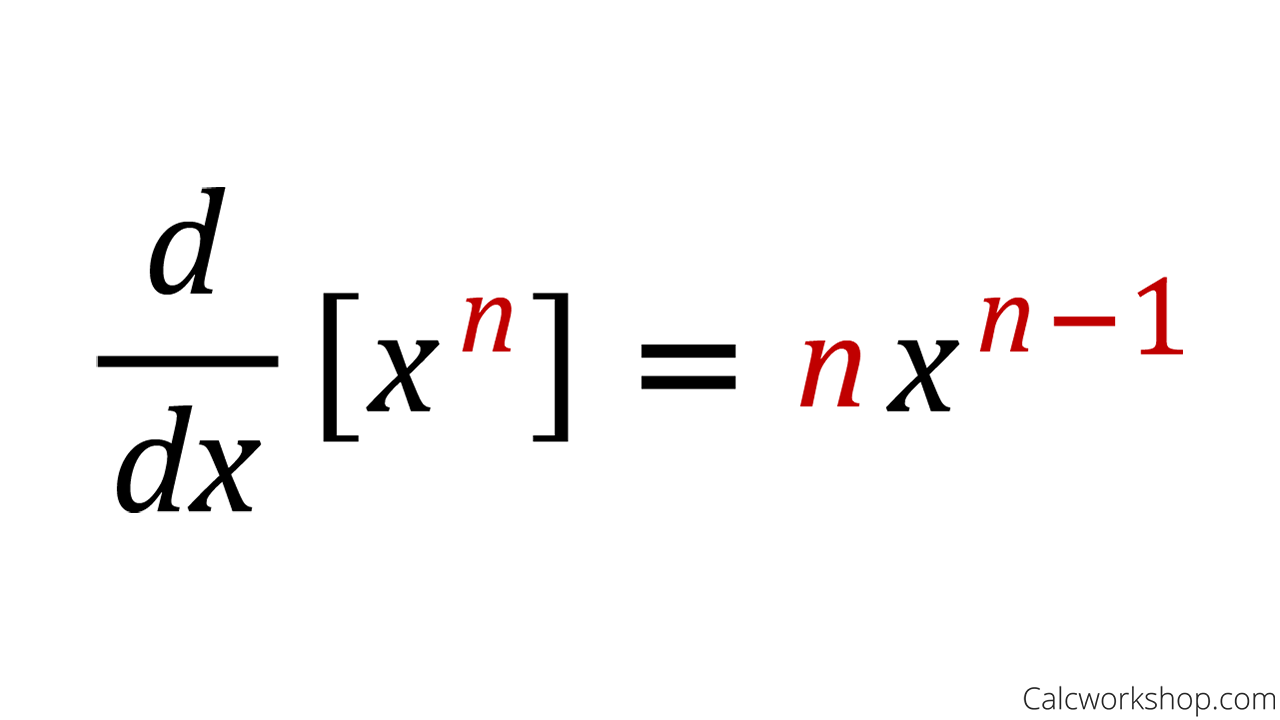
Now, for more applied example, let's look at a case involving slopes of curves, and in which you could theoretical in which you have an applied example. So let's suppose we have a truck let's make it a red truck, because why not? And then this truck has a few small wheels, and it also in a piece of wood sticking out of the back of the truck, this'll be important. We also have that the truck is going is tr is about to go up a hill and the Hills has satisfies the equation. The question is, can the truck make, and now the truck has the wood position in it, so that if the truck goes up at a, at an angle greater than 45 degrees, IE has a slope. Greater, goes up at a slope greater than one. The wood will fall out. The question is, will the wool wood fall out of the truck, out of the truck as it goes up to the hill. So to calculate this, we know that this is equal to zero. When a hundred equals. When we, when we set both sides of this to zero, this is equals zero. We have that. So then X squared equals 10,000. So X equals plus, or minus a hundred. So base here is negative a hundred and the truck is going up here.
So now the question is what is, so now let's see what the slope is at this point. So the slope X X equals negative a hundred. So the slope is going to just be the derivative of H to the X or equals D D X a hundred minus X squared, over a hundred, which equals zero minus two X, two minus one, over a hundred, which equals negative X over 50 and substituting in negative. A hundred for X gives us negative a hundred negative, a hundred over 50 or two. So it concludes since two is greater than one. We have the slope of the curve at X equals negative. A hundred is greater than one. Thus the incline is steeper than an incline of one corresponding to a slope of one, so steeper than 45 degrees. So the truck will indeed fall out.