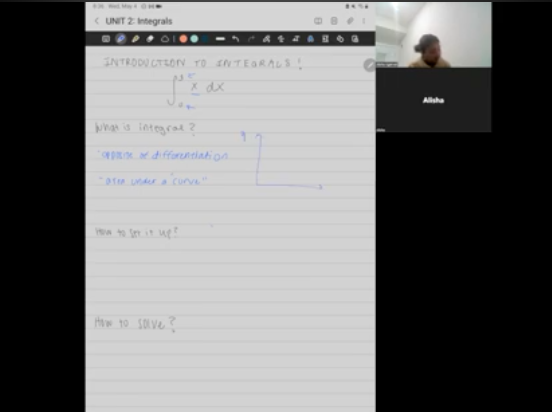
Hello everyone. Welcome back. We had a good weekend. We'll be starting this week off with learning about introduction to integrals and we'll be starting with the brief example of just integrating X from the lower bound of zero to upper bound three. So now might have just seen like a lot of your words too. You might not know half of what I've said, but we'll be starting with basic with what is in integral. So integral is the opposite of what we learned last week in that it is essentially the opposite of the differentiation. Instead of finding the slope of a function they did last week, essentially finding the area under a curve.
So what does this mean? That means if we grab the function here on a basic y X, we wanna grab this function X from the lower bound of zero to the upper bound of three. We have 1, 2, 3, 1, 2, 3. Then we're gonna graph this. So let's do a different color. So just use our basic algebra skills and grab that. And then we eventually wanna find, we call the area under the curve is this triangle we you right here. So we don't even need a calculus to be able to solve, but this integral is we can solve it by just knowing what the area of triangle is, right? So let's just do this for purposes of learning that we have one half times the three times the height, which is three and that's 0.5.

So then let's just use that as a crosscheck when we actually do the map. So how to set this up. So we have this weirdly line initially that indicates that we're gonna be taking the interval of something. Then when it has definite bounds, we would just set down with the lower bound of the bottom here and the upper bound at the top there. Then we put the function that we're integrating to the right of it, essentially inside of the integral. And then we have the extra tag at the end here, DX or D time, whatever other variable we're integrating with spec of. And that's just telling you which variable we're interested in integrating with respect to. So I'm here, it doesn't matter if it's clearly it would be the X, but sometimes uh, it's more prevalent if we have like X times Y or X times Y times B squared. And we wanna know what specific variable we should be finding the area underneath. Now how to solve this, it's pretty simple actually. So we have our zero three x D X, so we're thinking the opposite of the differentiation.
If you remember from last week, we would take the exponent of whatever variable we had and we would subtract one and then bring down the current expon to the base. Here we would be the opposite. So we have a one and the exponent there, so it's imaginary, um, but we don't really write it out. And here we were. So subtracting one as we word in differentiation we add one. So we have two and then we multiply the entire function by inverse. Um, the explan that we now have. So the inverse of two is one half and then we want to evaluate this from three to zero. We actually take the integral, the quickly line is replaced this bracket here and then we can just compute it as normal.
And then we get nine halve equals 4.5 which checks out above. And then as kind a cross check we can take the in just solved. We can make sure that that was correct by actually differentiating and seeing if we get back our original function that was inside of the integral. We differentiate this last week. We take the X down here where it's two times one half and then we take the X expon that we have and subtract it by one, but yet one times X to the one and that is x and that is what we had originally. So that is a basic introduction to integrals. Obviously this will get a lot more complicated as we deal with more, uh, complicated functions with exponents and logarithmic functions and monos. And we'll learn some more tricks and things that we can do with that. But for now, if you have any questions, please let me know and I'll be happy to answer them. Thank you.