When it comes to calculating the area of a trapezoid, many people may feel intimidated or unsure of where to begin. However, with a basic understanding of the trapezoid's properties and the appropriate formula, finding the area can be a relatively simple task. In this article, we will explain how to find the area of a trapezoid using the area formula trapezoid.

First, let's define what a trapezoid is.

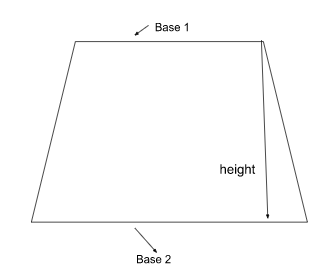
A trapezoid is a quadrilateral with at least one pair of parallel sides. The non-parallel sides are called the legs of the trapezoid, and the parallel sides are called the bases. In order to calculate the area of a trapezoid, we need to know the length of both bases and the height of the trapezoid.

GET $15 OF FREE TUTORING WHEN YOU SIGN UP USING THIS LINK

The formula for finding the area of a trapezoid is:

Area = (base1 + base2) x height / 2

In this formula, "base1" and "base2" refer to the lengths of the two parallel bases of the trapezoid, and "height" refers to the distance between the bases. The "/2" at the end of the formula is necessary because we are finding the area of a trapezoid, which has two non-parallel sides of different lengths.

Let's take a look at an example of how to use this formula. Suppose we have a trapezoid with a length of 6 inches for base1, a length of 10 inches for base2, and a height of 4 inches. To find the area of this trapezoid, we would plug these values into the formula:

💡
Area = (6 + 10) x 4 / 2
Area = 16 x 4 / 2
Area = 64 / 2
Area = 32 square inches

Therefore, the area of this trapezoid is 32 square inches.

It's worth noting that the formula for the area of a trapezoid can also be derived using a different method. We can split the trapezoid into a rectangle and two right triangles, as shown in the diagram below:

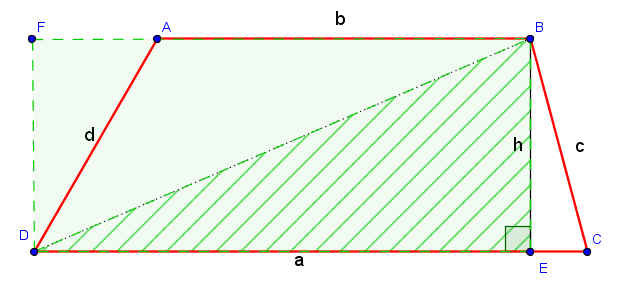
The area of the rectangle is simply base1 x height, while the area of each right triangle is base2 x height / 2. Adding these three areas together gives us:

💡
Area = base1 x height + 2 x (base2 x height / 2)
Area = base1 x height + base2 x height
Area = (base1 + base2) x height / 2

This is the same formula we derived earlier, but it may help to visualize how the formula works.

In some cases, we may not be given the height of the trapezoid.

However, we can still find the area if we know the lengths of both bases and at least one of the angles between the bases. To do this, we use the following formula:

💡
Area = (base1 + base2) x height / 2
Height = (base2 - base1) x tan(angle) / 2

In this formula, "angle" refers to the angle between the two bases, and "tan" is the tangent function. By plugging the lengths of the bases and the angle into this formula, we can find the height of the trapezoid, and then use the area formula trapezoid to find the area.

Let's look at an example of how to use this formula. Suppose we have a trapezoid with a length of 8 inches for base1, a length of 12 inches for base2, and an angle of 60 degrees between the bases. We can find the height of the trapezoid using the following formula:

💡
Height = (12 - 8) x tan(60) / 2
Height = 2 x sqrt(3) inches

Now that we know the height, we can find the area using the area formula trapezoid:

💡
Area = (8 + 12) x 2 x sqrt(3) / 2
Area = 20 x sqrt(3)
Area ≈ 34.64 square inches

Therefore, the area of this trapezoid is approximately 34.64 square inches.

How to Derive The Trapezoid Area Formula?

To derive the formula for the area of a trapezoid, we need to start by drawing a trapezoid and identifying its height and bases.

Let's say the trapezoid has a height of "h" and two parallel bases with lengths "a" and "b" respectively. We can divide the trapezoid into two smaller triangles and one rectangle, as shown below:

We can see that the area of the trapezoid is equal to the sum of the areas of these three shapes:

💡
Area of trapezoid = Area of rectangle + Area of triangle 1 + Area of triangle 2

Area of rectangle = a * h

The two triangles have equal heights (since they are halves of the same height) and bases a and b. The formula for the area of a triangle is:

💡
Area of triangle = (1/2) * base * height

Therefore, the areas of the two triangles are:

💡
Area of triangle 1 = (1/2) * a * h
Area of triangle 2 = (1/2) * b * h

Substituting these values into the formula for the area of the trapezoid, we get:

💡
Area of trapezoid = a * h + (1/2) * a * h + (1/2) * b * h

Simplifying this expression by factoring out h, we get:

💡
Area of trapezoid = h * (a + b) / 2

Therefore, the formula for the area of a trapezoid is:

💡
Area of trapezoid = (base1 + base2) / 2 * height

or

💡
Area of trapezoid = (a + b) / 2 * h

where "a" and "b" are the lengths of the two parallel bases, and "h" is the height of the trapezoid.

In conclusion, finding the area of a trapezoid is a straightforward process once you understand the formula. It's important to remember that we need to know the lengths of both bases and the height of the trapezoid in order to use the formula directly. However, if we only know the lengths of the bases and at least one angle, we can still find the height using the tangent function before using the area formula trapezoid.

One important thing to keep in mind is that the units of the bases and height must be the same in order to get a result in square units. For example, if the bases are measured in inches, the height must also be measured in inches. It's also a good idea to double-check your calculations to make sure you have entered the values correctly and used the correct formula.

In summary, the trapezoid area formula is an essential tool for calculating the area of trapezoids. With a bit of practice, you can quickly and easily find the area of any trapezoid you encounter. If you’re feeling stuck, then connect with a math tutor to help you through the process of calculating the area of a trapezoid.