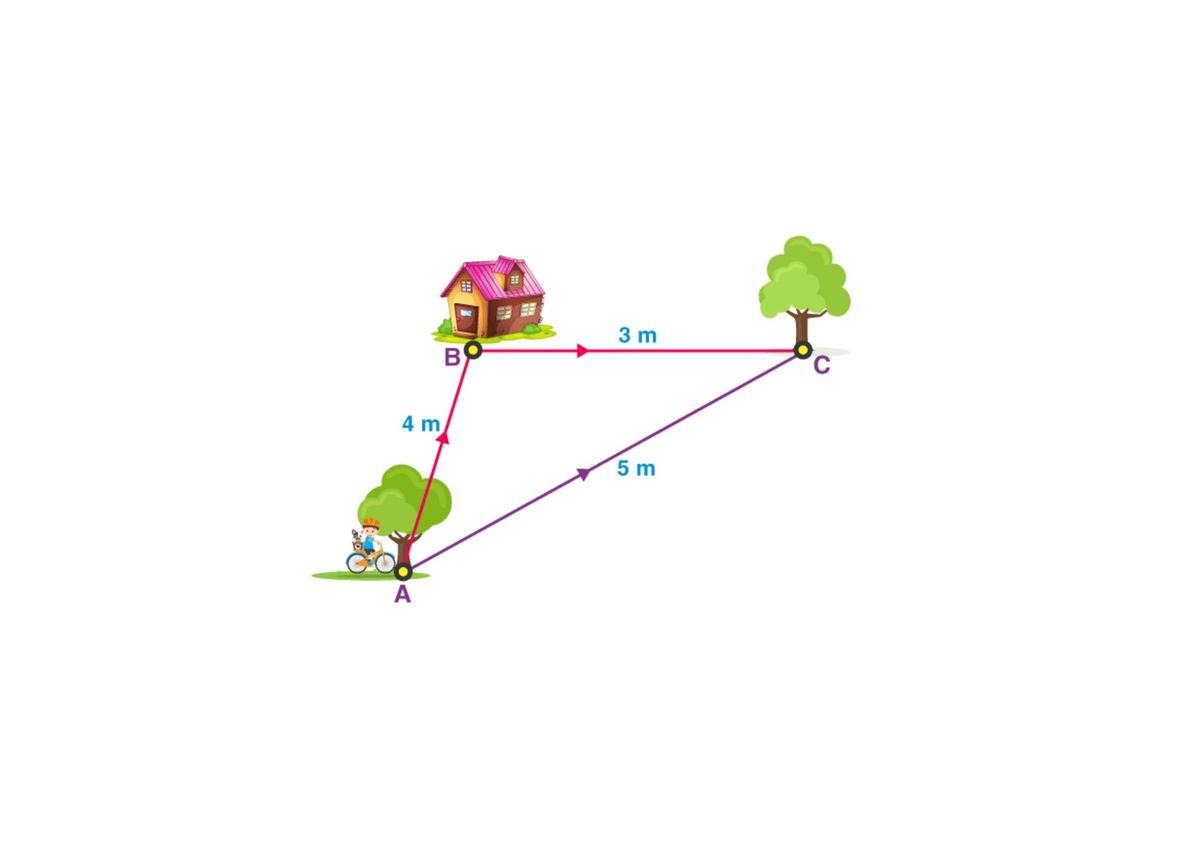
Distance formula is an essential mathematical tool used to determine the distance between two points in a Cartesian plane. The Cartesian plane is a coordinate system that comprises two perpendicular axes, the x-axis, and the y-axis.
The intersection of the axes is known as the origin, denoted as (0, 0). Any point in the plane can be represented by a unique ordered pair of coordinates (x, y). The distance formula is derived from the Pythagorean theorem and is used in various fields such as mathematics, physics, and engineering.
The distance formula is given as:
Where d is the distance between two points, (x1, y1) and (x2, y2) are the coordinates of the two points.
The distance formula can be applied to various problems, including finding the distance between two points in a straight line or the distance traveled by an object in motion. In this article, we will explore the distance formula and its applications in various fields.
Deriving the Distance Formula
The distance formula is derived from the Pythagorean theorem, which states that in a right-angled triangle, the sum of the squares of the two shorter sides is equal to the square of the longest side (the hypotenuse). Consider a right-angled triangle with vertices at points A (x1, y1), B (x2, y2), and C (x2, y1), as shown below.
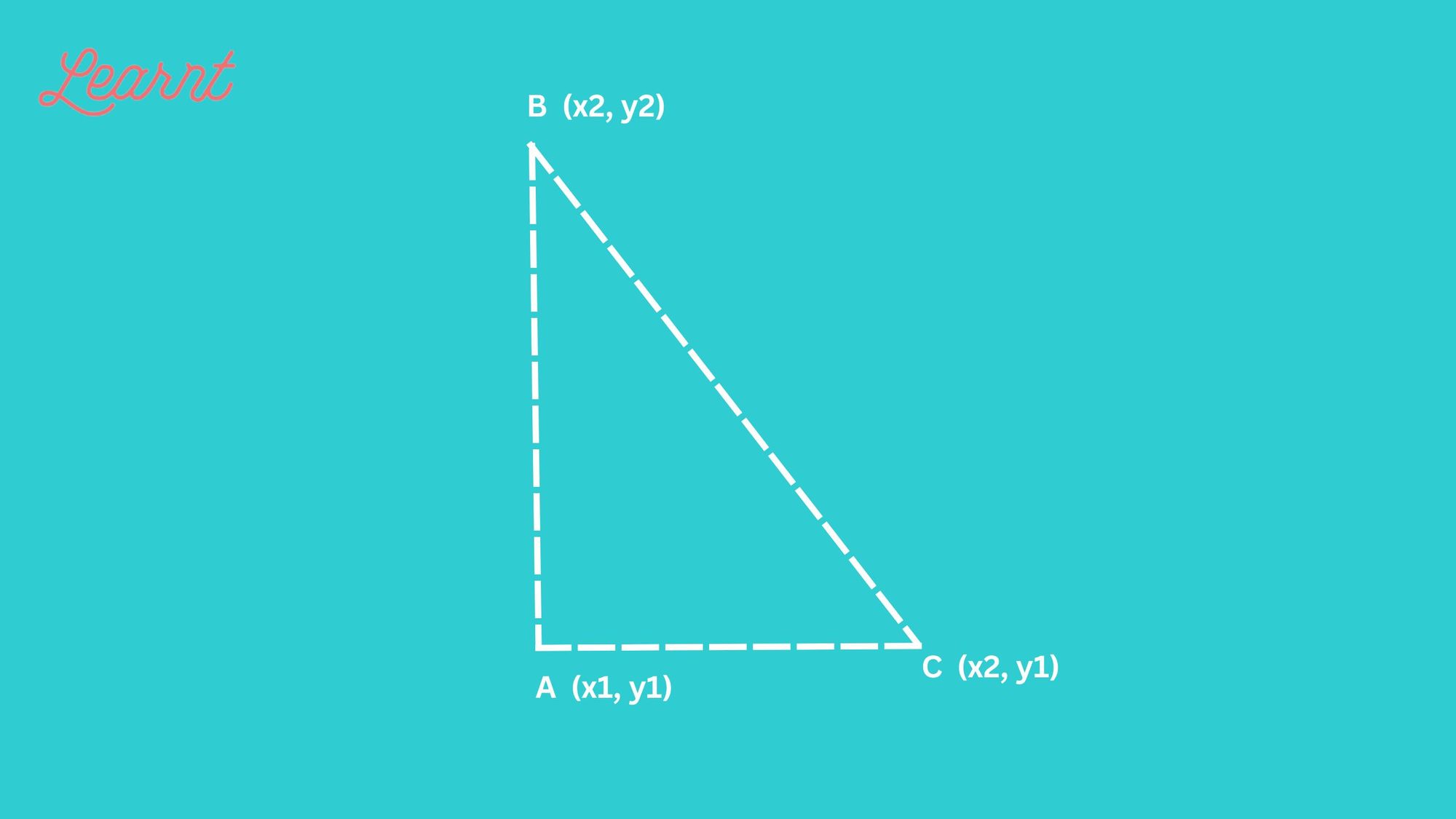
et d1 be the distance between A and C, and d2 be the distance between B and C. We can express d1 and d2 using the Pythagorean theorem as follows:
d1 = √((x2 – x1)² + (y1 – y1)²)
d2 = √((x2 – x2)² + (y2 – y1)²)
Since C is a common point in both triangles, we can express the distance AB as the difference between d1 and d2 as follows:
AB = d1 – d2
Substituting d1 and d2 into the equation, we get:
AB = √((x2 – x1)² + (y1 – y2)²)
Rearranging the equation, we get the distance formula:
d = √((x2 – x1)² + (y2 – y1)²)
Applications of the Distance Formula
The distance formula is a versatile tool that has various applications in different fields. Some of these applications are discussed below.
- Finding the Distance Between Two Points
One of the most common applications of the distance formula is finding the distance between two points in a Cartesian plane. Suppose we have two points A (x1, y1) and B (x2, y2). We can use the distance formula to calculate the distance between these two points as follows:
d = √((x2 – x1)² + (y2 – y1)²)
For example, suppose we have two points A (2, 3) and B (5, 7). We can use the distance formula to find the distance between these two points as follows:
d = √((5 – 2)² + (7 – 3)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
2. Calculating the Distance Traveled by an Object
The distance formula can also be used to calculate the distance traveled by an object in motion. Suppose an object moves from point A (x1, y1) to point B (x2, y2). We can use the distance formula to calculate the distance traveled by the object as follows:
d = √((x2 – x1)² + (y2 – y1)²)
For example, suppose a car moves from point A (2, 3) to point B (5, 7) in a straight line. We can use the distance formula to calculate the distance traveled by the car as follows:
d = √((5 – 2)² + (7 – 3)²)
d = √(3² + 4²)
d = √(9 + 16)
d = √25
d = 5
Therefore, the car traveled a distance of 5 units.
3. Calculating the Magnitude of a Vector
The distance formula can also be used to calculate the magnitude of a vector. In mathematics, a vector is a quantity that has both magnitude and direction. The magnitude of a vector is its length and is calculated using the distance formula. Suppose we have a vector v with components (a, b). The magnitude of the vector is given as follows:
|v| = √(a² + b²)
For example, suppose we have a vector v with components (3, 4). We can use the distance formula to calculate the magnitude of the vector as follows:
|v| = √(3² + 4²)
|v| = √(9 + 16)
|v| = √25
|v| = 5
Therefore, the magnitude of the vector v is 5 units.
4. Finding the Midpoint of a Line Segment
The distance formula can also be used to find the midpoint of a line segment. The midpoint of a line segment is the point that is equidistant from the two endpoints of the segment. Suppose we have a line segment AB with endpoints A (x1, y1) and B (x2, y2). The midpoint of the line segment is given as follows:
((x1 + x2)/2, (y1 + y2)/2)
For example, suppose we have a line segment AB with endpoints A (2, 3) and B (5, 7). We can use the distance formula to find the midpoint of the line segment as follows:
Midpoint = ((2 + 5)/2, (3 + 7)/2)
Midpoint = (3.5, 5)
Therefore, the midpoint of the line segment AB is (3.5, 5).
5. Calculating the Area of a Triangle
The distance formula can also be used to calculate the area of a triangle. Suppose we have a triangle with vertices at points A (x1, y1), B (x2, y2), and C (x3, y3). The area of the triangle is given as follows:
Area = 0.5 * |(x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2))|
For example, suppose we have a triangle with vertices at points A (2, 3), B (5, 7), and C (7, 4). We can use the distance formula to calculate the area of the triangle as follows:
Area = 0.5 * |(2(7 – 4) + 5(4 – 3) + 7(3 – 7))|
Area = 0.5 * |(6 + 5 – 16)|
Area = 0.5 * |-5|
Area = 2.5
Therefore, the area of the triangle with vertices at points A (2, 3), B (5, 7), and C (7, 4) is 2.5 square units.

Conclusion
In conclusion, the distance formula is an important tool in mathematics and physics. It allows us to calculate the distance between two points in a coordinate plane and is used in various applications such as finding the distance traveled by an object, calculating the magnitude of a vector, finding the midpoint of a line segment, and calculating the area of a triangle.
The formula is simple to use and can be applied to solve a wide range of problems. By understanding and mastering the distance formula, students can improve their problem-solving skills and develop a deeper understanding of mathematics and physics concepts.