Introduction
The unit circle is a fundamental concept in trigonometry that is used to understand the relationship between angles and their trigonometric functions. Understanding the unit circle is essential for students studying trigonometry, calculus, and other advanced mathematics courses. In this article, we will explore the basics of the unit circle and delve into more advanced topics to provide a comprehensive guide to this important concept.
What is the Unit Circle?
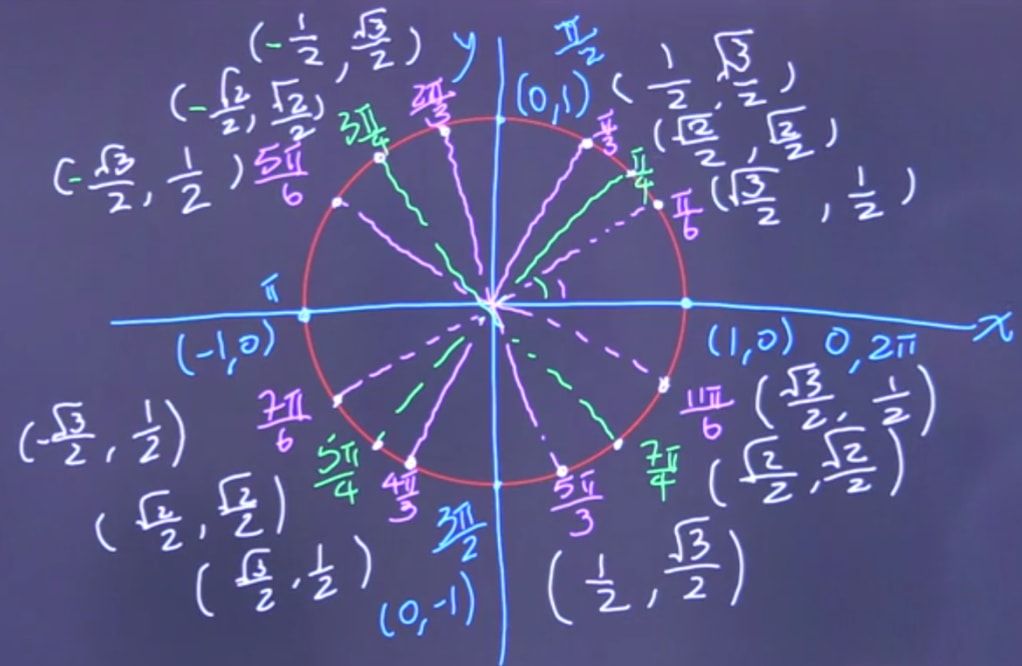
The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. The circle is divided into 360 degrees or 2π radians, with each degree or radian corresponding to a point on the circle. The unit circle can be thought of as a reference point for measuring angles and their corresponding trigonometric functions.

Trigonometric Functions on the Unit Circle
The six trigonometric functions - sine, cosine, tangent, cosecant, secant, and cotangent - can be defined using the coordinates of a point on the unit circle. These functions are calculated using the ratios of the lengths of the sides of a right triangle, with one side being the radius of the circle and the other two sides being the coordinates of the point on the circle.
For example, the sine of an angle θ is equal to the y-coordinate of the point on the unit circle that corresponds to that angle. Similarly, the cosine of θ is equal to the x-coordinate of the point, and the tangent of θ is equal to the ratio of the sine and cosine.
Using the unit circle, we can quickly calculate the values of the trigonometric functions for standard angles. For example, the sine of 30 degrees is equal to 0.5, and the cosine of 45 degrees is equal to √2/2.
Degrees vs. Radians
Degrees and radians are two common units for measuring angles. Degrees are based on dividing a circle into 360 equal parts, while radians are based on dividing a circle into 2π equal parts. One radian is equal to 180/π degrees, or approximately 57.3 degrees.
Radians are often used in calculus and other advanced mathematics courses because they provide a more natural unit for measuring angles in circular functions. Many trigonometric identities and calculus formulas are written in terms of radians, and using radians can simplify many calculations.
Converting between degrees and radians is straightforward, as one full rotation around the unit circle is equal to 360 degrees or 2π radians. To convert from degrees to radians, multiply the degree measure by π/180. To convert from radians to degrees, multiply the radian measure by 180/π.
Advanced Concepts in the Unit Circle
In addition to the basic trigonometric functions, there are many advanced concepts that involve the unit circle. These include inverse trigonometric functions, trigonometric identities, and the use of the unit circle in calculus.
Inverse trigonometric functions are used to find the angle that corresponds to a given value of a trigonometric function. For example, the inverse sine function returns the angle whose sine is equal to a given value. Inverse trigonometric functions are useful for solving equations involving trigonometric functions and for finding angles in real-world applications.
Trigonometric identities are equations that are true for all values of the variables involved. These identities are used to simplify complex expressions and to prove other mathematical results. The unit circle can be used to derive many of these identities, such as the Pythagorean identity, which states that sin²θ + cos²θ = 1.
The unit circle is also used in calculus to find the derivatives and integrals of trigonometric functions. By understanding the properties of the unit circle, we can derive many of the formulas used in calculus, such as the derivatives of sine and cosine, and the fundamental theorem of calculus.
Applications of the Unit Circle
The unit circle has numerous applications in mathematics, science, and engineering. It is used in physics to describe the motion of objects in circular motion, such as planets in orbit. In engineering, the unit circle is used to design machines and structures that involve rotating components.
In addition, the unit circle is used in many fields of science to study wave phenomena, such as sound and light. The sine and cosine functions can be used to describe the behavior of waves, and the unit circle provides a way to visualize and understand these phenomena.
Real-World Examples
The unit circle can be used to solve real-world problems involving trigonometry. For example, consider a construction project that involves building a ramp for a wheelchair. The ramp needs to have a slope of no more than 1:12, which means that for every 12 inches of horizontal distance, the ramp can rise no more than 1 inch.
To determine the angle of the ramp, we can use the inverse tangent function. If the horizontal distance of the ramp is 144 inches, we can find the angle by calculating the inverse tangent of 1/12, which is approximately 4.76 degrees. This angle can then be used to design the ramp to meet the required specifications.
Conclusion
The unit circle is a fundamental concept in trigonometry that provides a way to understand the relationship between angles and their trigonometric functions. By understanding the properties of the unit circle, we can derive many important formulas in calculus and other advanced mathematics courses. The unit circle also has numerous applications in science, engineering, and real-world problem-solving. Whether you are studying trigonometry for the first time or are a seasoned mathematician, a solid understanding of the unit circle is essential for success in advanced mathematics.